Beyond the sea
In the northern reaches of Newfoundland, near the town of St. Anthony, is the Fox Point Lighthouse. I’ve never been there, but I know it has one of the most impressive ocean views in the world. If you face perpendicular to the right bit of rocky coastline there and gaze straight across the ocean, your mind’s eye peering well beyond the horizon, you can see all the way to Australia.
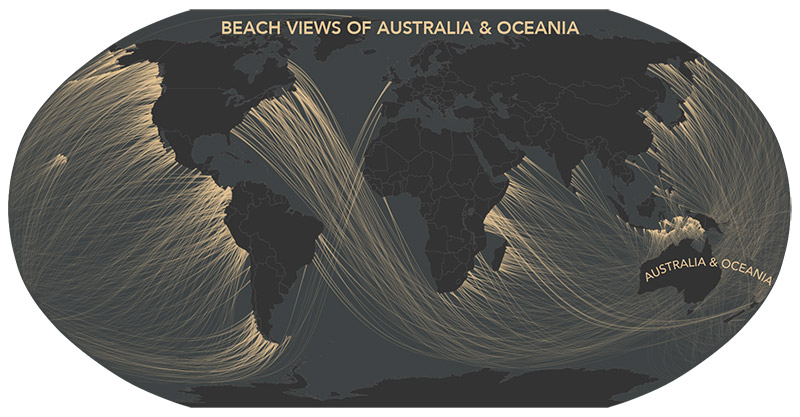
What’s really across the ocean from you when you look straight out? It’s not always the place you think.
I’m inspired by a map done a couple of years ago by Eric Odenheimer and some follow-ups by Weiyi Cai and Laris Karklis of the Washington Post. Those maps are colorful, handy guides to countries of equivalent latitude across the oceans. It’s easy to forget, for example, that much of Europe is well north of the United States east coast. But they’re not exactly maps of what’s across the ocean from you, at least not directly across from you. To think of east or west as “straight” across is, perhaps, one of those effects of the map projections we see every day.
The latitude maps got me interested in answering the question more strictly: standing on a given point and facing perpendicular to the coast, if you went straight ahead, never turning, where would you end up? There are two reasons why following a line of latitude won’t answer the question.
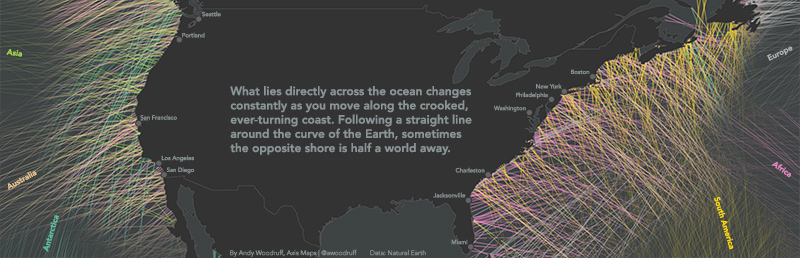
1. Coastlines are crooked and wacky.
2. The earth is round.
With that in mind, here are some maps showing the points from which you can “see” each of the continents.
Coastline angle
Coastlines face all different directions, bending and turning constantly. The “East coast” isn’t a straight north-south line facing directly east. Just look at the state where I live, which has coastline facing literally all directions.
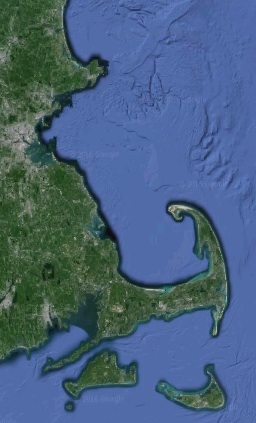
Taking “across the ocean” to mean directly across, perpendicular to the coast, then what’s across the ocean depends on where you’re standing! To get a rough idea of what direction the world’s coastlines face, I’m calculating the angle between every pair of adjacent coastal vertices in medium scale Natural Earth data, then placing a point in between them and measuring the view from there based on that angle.
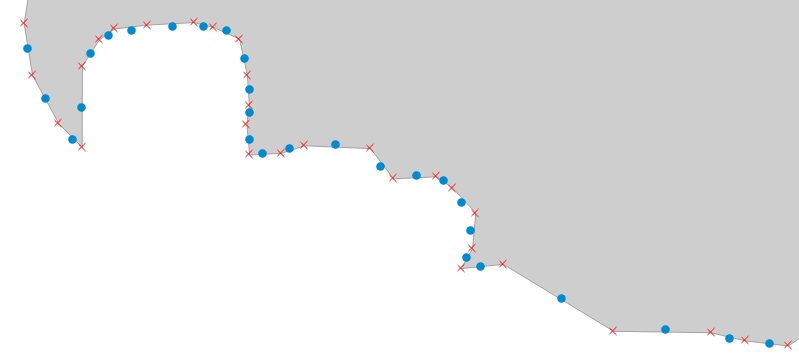
The much-maligned Mercator projection comes in handy here. Those angle calculations were made using projected coordinates because the conformal Mercator projection preserves the thing I’m interested in: local angles!
Straight lines on a round object
The second point is trickier to imagine thanks to common rectangular maps and the way latitude itself is defined. If you can detach the concept of “direction” from the concept of east and west, and look at globes and other map projections, it’s easy enough to picture. The shortest, straightest line on a sphere (let’s call the Earth a sphere even though it technically isn’t) is a great circle arc, not something like a line of latitude.
What we often think of as “straight” is a path following a rhumb line, a line of constant bearing. Wikipedia succinctly describes how such a “straight” line actually turns, in contrast to a great circle.
If one were to drive a car along a great circle one would hold the steering wheel fixed, but to follow a rhumb line one would have to turn the wheel, turning it more sharply as the poles are approached.
A typical classroom demonstration of great circles is to pull a piece of string taut on the surface of a globe between two points, and note how the string arcs across lines of latitude, changing its bearing the whole way. Try this specific case to drive home how the spherical “straight” differs from “straight” as we’ve defined compass directions: find a line of longitude on the globe, then a spot along that line somewhere away from the equator. Bring the globe to your eye and place the string perpendicular to the meridian, in between two latitude lines. Line up your view with the string and you can see that even though it starts out going due east or west, as it continues directly ahead the “straight” east/west parallels curve away from it.

So if we want to know what’s truly straight across the ocean from a given coastline point, we need to see what direction the coast faces at that point, then draw a great circle in that direction and see what it runs into.
As for flat maps, certain map projections provide an accurate view of directions. The azimuthal equidistant projection, for example, preserves correct direction (and distance) from the center point of the map. A straight line from the center of the map is a straight line in real life. Here’s the Newfoundland-to-Australia example from earlier:
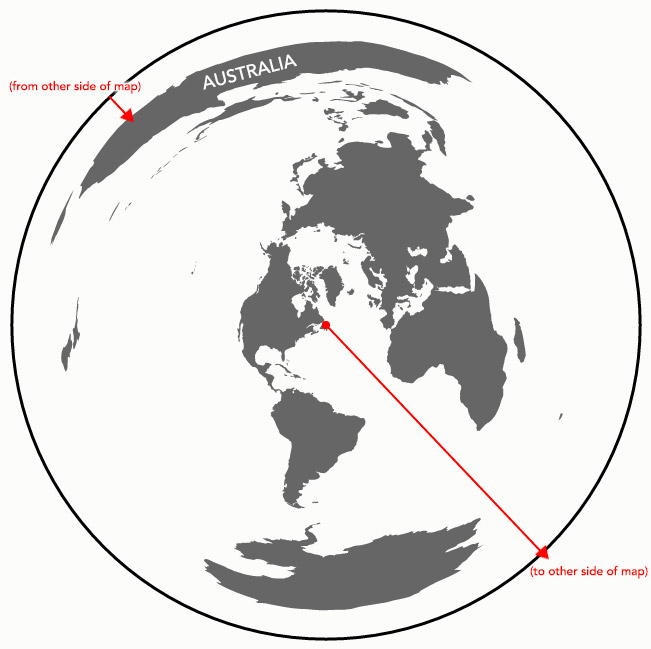
Such a map, in the end, is how I’m figuring out beach views: center that projection on each point, then draw a straight line in the correct direction until it hits land.
Conclusion
I’m not entirely certain that I have all the math right, but I think it’s at least close. Even we cartographers sometimes have a shaky grasp of map projections and spherical geometry.
But who has time for correct math? I’ve got to start training for the straight-line swim from the number one beach in my life—30th Street in Ocean City, New Jersey—to Brazil.


50 Comments