Raster map projection with ActionScript 3
This is probably a stupid idea, but that’s never stopped me before.
Lately some of my Flash mapping colleagues and I have come to rely on transforming geographic data—say, shapefiles—into various map projections on the client side via the ActionScript vector drawing methods. (See, for example, a post by my friend Zachary Johnson with an old-as-the-hills demo. And don’t you worry: we’ll be releasing something way, way cooler eventually.) But as cartographers know, vector data is just one side of things. What about raster data?
These days Flash allows good pixel-level manipulation of raster images with the BitmapData class. As a cartographer, I thought I’d try a little experiment in map projections.
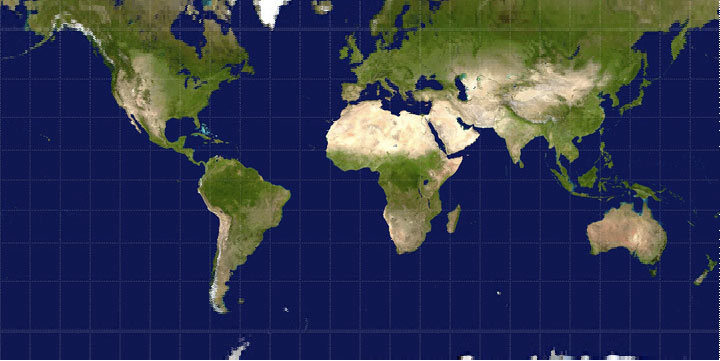
The goal: Convert an “unprojected” (plate carrée) world map map to a Winkel Tripel projection. I used an image from Wikipedia as a starting point.
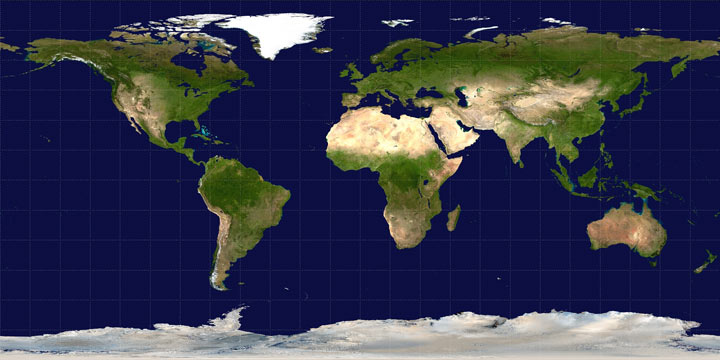
This is what we want to end up with:

Not terribly long ago for a mapping project I wasted a ridiculous amount of time on someone else’s dime attempting to reproject a raster map using the ActionScript DisplacementMapFilter class. If you don’t know, what the DisplacementMapFilter does is use the colors on a displacement map image (a BitmapData object) to determine displacement of pixels on another object. One color channel determines the x displacement and another the y displacement, both relative to the midpoint in the range of values for that color (i.e., 127 out of 255). For example, if we use the red channel for x and the blue channel for y, and a pixel in the displacement map has a red value of 255 and a blue value of 0, the corresponding pixel in the target object will be displaced positively 100% in the x direction and negatively 100% in the y direction. The actual number of pixels that 100% represents depends on a specified scale factor.
For a map projection, then, what we have to do is go through the unprojected source image pixel by pixel and determine how far each pixel has to be displaced on both axes by plugging the latitude and longitude values for the pixel into a projection formula. Using red for the x displacement and blue for the y displacement, below is the displacement map I generated for turning the unprojected map into Winkel Tripel.

I then applied that to the source image. The result? Yuck.
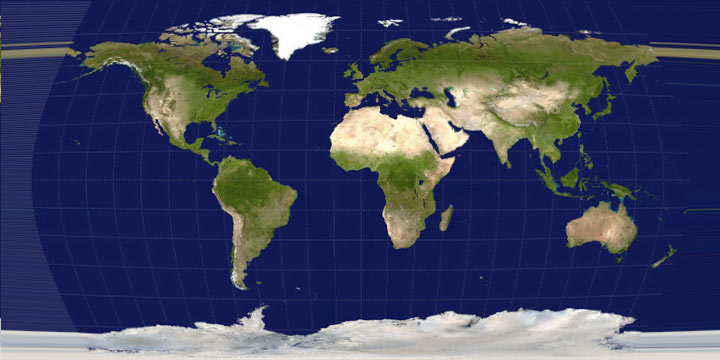
It’s probably possible to mess with this method and produce better results. As previously suggested, though, I’ve already spent too much time doing that without coming up with anything decent. In my experience there are three drawbacks to using the DisplacementMapFilter for map projections: (1) because of the way the filter works, if what you know ahead of time is the exact distance that pixels need to be displaced, it seems to be necessary to iterate over every single pixel twice, once to determine the maximum displacement in each direction for the entire image and once to then actually draw the displacement map; (2) precision in displacement is very limited, as it can only be from 0 to 127, in whole numbers, in either direction (multiplied by the scale factor); and (3) some projections will result in larger images than the original unprojected map, and it is a nuisance to try to deal with those using this method.
Screw it, then. Why not just move the pixels manually? To do this, we basically look at each pixel in the source image, run its latitude and longitude through the projection formula to determine its new location on the projected map, and then draw that pixel on the projected map with the color of the source pixel. Here’s what happened when I did that:
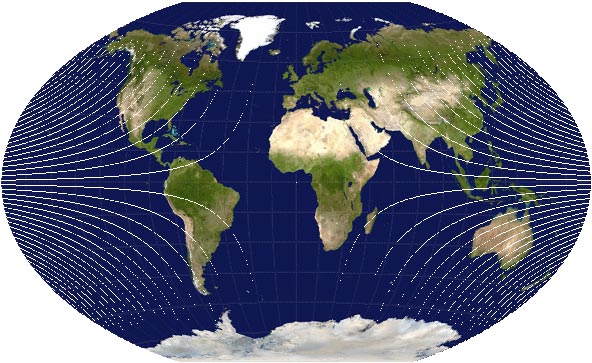
Hey, it’s the correct shape! But there are two issues with distorting a map to project it, namely, that the map is going to be compressed in some places and stretched in others. I’ve already attempted to deal with the compression in the above image. Instead of directly transferring the color of a source pixel to the projected map, I kept track of all the source colors that corresponded to a pixel on the projected map, then drew the average color on that projected pixel. Otherwise, when more than one source pixel corresponds to a projected pixel, the color would just be replaced every time one of those source pixels is encountered. In this case it was actually difficult to see much difference, but the attempt at resampling seemed like a good idea.
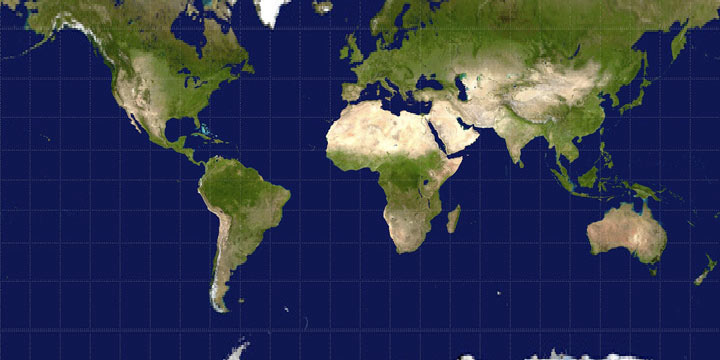
The second issue, the stretched parts, is evident in the above map, showing up as those white (empty) curves emanating from the edges. That occurred where pixels on the projected map had no corresponding source pixel because of distance distortions in the projection. To correct for this I did a simple interpolation in which I identified pixels with no data and assigned each a color that was the average of any neighboring colors. With that, then, we have our final map:

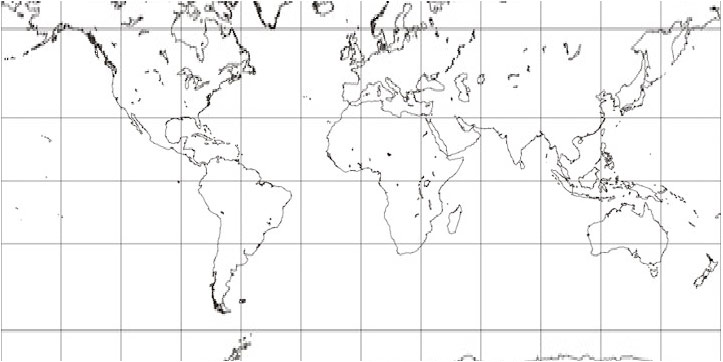
It’s not the most beautiful map, but not too bad, I’d say. That’s just one type of projection, though. As you might expect, the more interpolation that’s needed, the worse it’s going to look with these methods. Below, for example, is part of a Mercator projection. (Remember how I said larger map projections are a nuisance with the DisplacementMapFilter? Well, they’re kind of a nuisance in general, hence “part of” a map here.) The Mercator projection stretches the map pretty significantly in high latitudes, and as you can see the map doesn’t look very good near the top and bottom.
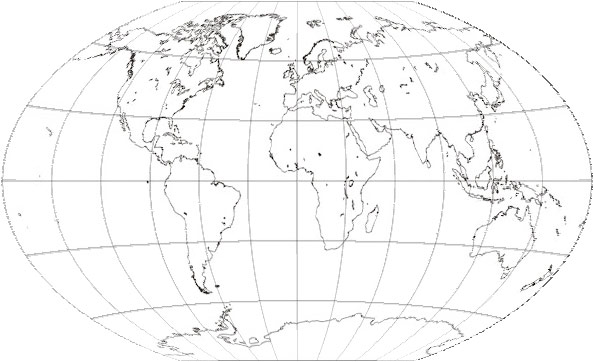
It’s also worth noting that these raster methods are probably best with continuous images like the example used here. The flaws are more noticeable with a rasterized line map, as below (projected using a source image from the wonderful Gallery of Map Projections).
And Mercator’s not so hot:
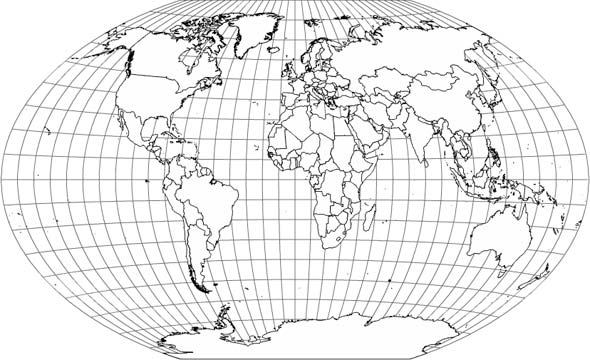
For the record, here’s what a nice, scalable, vector map projection from a shapefile looks like in Flash:
This little experiment has demonstrated that reprojecting raster maps in ActionScript is possible, perhaps with acceptable results in a pinch, but it’s far from perfect. I don’t doubt that it would be possible to use more advanced resampling and interpolation methods, but this is already a lot to deal with. The projections here took several seconds to compute and draw on my machine. That’s probably already an eternity in computer time, especially for a relatively small image, and it’s only going to grow as the algorithm becomes more complex. (Okay, minus the time that would be saved if my surely inefficient code were improved.) This kind of thing isn’t Flash’s strong suit anyway, right? Real geographic raster processing is being done with things like GDAL.
But again: in a pinch, it works!
Some references:
- The aforementioned Gallery of Map Projections is a good resource for seeing what different projections look like.
- This Java applet demonstrating map projections appears to use a raster map, though I’m not entirely sure how it operates. The source code is available.
- For map projection formulas, I recommend Wolfram Mathworld or Wikipedia.
- If you have access to the journal Cartographic Perspectives, check out Number 59 (Winter 2008) to see a gallery artistic renderings of map projection distortions by daan Strebe. The displacement map image used in this post reminded me of those images, which were presented at the 2007 NACIS conference.
Tagged as3, projections

9 Comments